Sizing Hollows and Rounds

Sizing Hollows and Rounds by Kenneth F. Greenberg

Hollows and rounds are among the most common of wooden planes – probably the most common outside of bench planes (jacks, smoothers, jointers, etc.). Most put them in the general category of molding planes, although there are those who feel they are a separate category unto themselves. I will avoid this philosophical debate since the purpose of this article is to discuss a different topic that often comes up in old tools circles: what do the size numbers on these planes really mean?

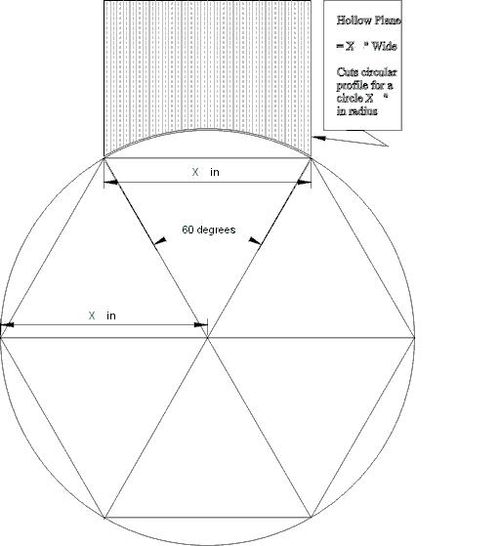
First off, it is useful to understand the relationship between the size of one of these planes and the size of the circle to which it is related. I use this terminology because a hollow (the concave plane) does not actually cut a circle in normal use, but rather the outside arc of a circle. Similarly, the round (the convex plane) cuts an inside arc. Traditional hollows and rounds cut an arc equal to one-sixth of a circle. Why was this chosen as a standard?

While plane makers were probably better craftsmen than mathematicians, there is a very practical aspect to this choice. Without getting into any geometrical proofs, a good basic understanding of this principle is quite easy to grasp. Suppose you took a circle and divided it up into six equal portions, marking off six points on the circle to indicate where they were. Now, connect each point to its neighbor. You have just inscribed a hexagon in the circle. If you then connected each point to the center of the circle, you have divided the hexagon into six triangles which can be proved to be equilateral. That means that the distance between two neighboring points on the circle is exactly the same as the radius of the circle.

Now think about a plane designed to match the profile of the outside of the circle from one point to the next, as shown above. The width of the plane iron would be the same as the distance between two adjoining points on the circle. So if you wanted to cut a circle of one-inch radius (or two-inch diameter), you just reached for a plane with an iron width of one inch. What could be simpler? This only works if the arc of the iron is one-sixth of a circle, so it is easy to see why this became a standard.

So much for the easy part. Now we need to consider the actual size numbers stamped on the plane itself. These do not, unfortunately, have a very good correspondence with the size of the plane. Each manufacturer numbered their planes from smallest to largest, with numbers chosen to indicate the relative position of a plane within a full set. Planes were frequently sold as pairs or individually, but sometimes were sold as either a full set or half set. A full set included a pair of each size; a half set usually included only the even-numbered pairs of planes.

The problem here is that each manufacturer chose his own numbering system, and so plane size numbers do not often match from one manufacturer to the next. Some copied the numbering system of some other manufacturers, and some companies had more than one numbering system. This was sometimes due to two companies merging (e.g., Ohio Tool and Auburn) or just a different way of doing things in a different era.

Further, some companies did not offer half sets (Ohio Tool is a good example), but simply offered planes only in those sizes that corresponded to the members of a half set. Typically, these planes would increase in iron widths by about 1/8 inch from one marked number to the next. I tend to call this "coarse granularity." This is a common trait among Ohio plane makers; Sandusky uses identical sizing in their 1925 catalog. In contrast, most of the New England makers did offer full and half sets (or at least number their planes according to such a scheme), providing "fine granularity." The difference between two consecutive size numbers in such a scheme would then be 1/16 inch. This is true of the smaller size planes but not necessarily the larger ones, as we shall see.

Why should such a regional difference exist? This is pure speculation on my part, but it should be remembered that in the first half of the 19th century, Ohio was still considered part of the Western frontier. The area around Sandusky was not settled until the 1820's when a group of "immigrants" from Connecticut arrived. In the last half of the century - the "golden age" of wooden plane making - Ohio was starting to be what we call it today, the Midwest. But it still was mostly rural and agrarian. Most of the work done in Ohio was probably functional furniture for everyday use. New England had developed into a center for furniture design, and its more established cities were demanding more ornate furniture for the well-to-do. These had more complex design details and required more exact tools to meet those requirements.

The following table contains data from an Ohio Tools catalog and provides an example of coarse granularity. It is interesting to note that they sold a set that consisted of pairs 1 through 9, but larger sizes had to purchased as pairs of planes and were not included as part of a set. The larger sizes also carried a different model number (73) from the more common smaller sizes (model 72).

Number	Iron width	Circle Diameter
1	¼	½
2	3/8	¾
3	½	1
4	⅝	1 ¼
5	¾	1 ½
6	⅞	1 ¾
7	1	2
8	1 1/8	2 ¼
9	1 ¼	2 ½
10	1 ⅜	2 ¾
11	1 ½	3
12	1 ⅝	3 ¼
13	1 ¾	3 ½
14	1 ⅞	3 ¾
15	2	4